Materi Beserta Soal Dan Pembahasan Jembatan Wheatstone Secara Lengkap
Pengertian Jembatan Wheatstone
Jembatan Wheatstone adalah sebuah rangkaian elektrikal yang digunakan untuk mengukur resistansi listrik yang tidak diketahui dengan membandingkannya dengan resistansi yang diketahui. Jembatan ini dinamai dari fisikawan Britania, Sir Charles Wheatstone, yang pertama kali menggambarkan konsepnya pada tahun 1843.
Prinsip dasar dari jembatan Wheatstone adalah bahwa arus listrik akan mengalir melalui rangkaian terkecil (path) menuju tanah, mengikuti jalur resistansi terendah. Ketika sebuah jembatan Wheatstone seimbang, tidak ada arus yang mengalir melalui galvanometer atau meter arus yang terhubung ke titik tengah rangkaian, sehingga menunjukkan bahwa resistansi di kedua sisi jembatan tersebut sama.
Jembatan Wheatstone biasanya terdiri dari empat resistor yang diatur dalam dua rantai paralel dengan resistor yang tidak diketahui yang dihubungkan di antara dua titik dalam rangkaian. Ketika jembatan seimbang, perbandingan antara resistansi-resistansi dalam dua rantai paralel dapat digunakan untuk menghitung resistansi yang tidak diketahui.
Jembatan Wheatstone telah banyak digunakan dalam berbagai aplikasi teknik, termasuk dalam pengukuran berat, pengukuran suhu, dan pengukuran tekanan. Meskipun mungkin telah banyak digantikan oleh teknologi digital modern dalam beberapa aplikasi, konsep dasar jembatan Wheatstone tetap menjadi dasar bagi berbagai alat ukur presisi.
Baca Juga: Sebuah Sepeda Motor Bergerak Dengan Kecepatan Sebesar 36 Km/Jam
Gambar Jembatan Wheatstone
Gambar di bawah ini bentuknya sedikit berbeda tapi sejatinya sama. Gambar tersebut adalah susunan jembatan Wheatstone.
Contoh rangkaian untuk jembatan listrik selain jembatan wheatstone yaitu
jembatan Wien, jembatan Kelvin, dan lain sebagainya. Rangkaian jembatan
pada umumnya digambarkan seperti pada gambar di bawah.
Pada gambar di atas dijelaskan bahwa penyusun X1, X2, X3, dan X4 adalah komponen listri resistor, kapasitor, induktor, ataupun gabungan dari ketiganya. Sedangkan penyusun G yaitu Galvanometer yang berperan aktif sebagai rangkaian jembatan.
Cara Menentukan Hambatan Pengganti
Jadi ketika untuk mendapatkan besarnya suatu hambatan pengganti pada tiap susunan hambatan jembatan Wheatstone dapat memakai aturan dan juga rumus berikut:
1. Apabila perkalian silang antara R1 dan R3 sama dengan R2 dan R4 maka R5 bisa diabaikan sampai hanya menjumlah secara seri lalu dipararelkan.
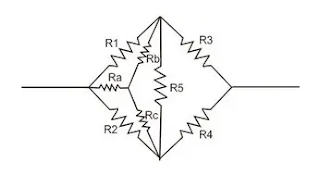
2. Apabila perkalian silang antara R1 dan R3 tidak sama dengan perkalian antara R2 dan R4. Maka hambatan harus diganti dengan hambatan baru sampai susunan hambatannya menjadi seperti di bawah ini.
Keterangan
Apabila R1, R2, dan R5 diganti dengan Ra, Rb, dan Rc. Sampai susunan menjadi seperti di bawah ini.
Kemudian hanya melanjutkan dengan prinsip seri dan pararel hambatan untuk menemukan hambatan penggantinya.
CONTOH SOAL DAN PENYELESAIAN JEMBATAN WHEATSTONE
Soal 1. Perhatikan gambar berikut!
Penyelesaian Fisika:
Sesuai dengan prinsip Wheatstone, arus yang berada di R3 sama dengan nol, jika memenuhi syarat :
Soal 2: Dibangun sebuah rangkaian jembatan yang tidak seimbang. Hitunglah beda tegangan keluaran pada titik C dan titik D dan nilai hambatan yang harus diseri dengan resistor R4 untuk menyeimbangkan menjadi rangkaian jembatan Wheatstone.
Untuk cabang ACB.
Soal 3: Gambar berikut adalah rangkaian jembatan Wheatstone, dengan panjang kawat homogen AB adalah 1 m. Ketika kontak geser C sedemikian sehingga jarak CB = 60 cm maka jembatan seimbang (Galvanometer G menunjuk nol). Jika ada X disisipkan seri resistor 10 Ω, maka jembatan seimbang ketika kontak C digeser sejauh 30 cm dari kedudukan seimbang semula. Tentukan nilai X dan Y!
AB = 1 m = 100 cm.
Pada kedudukan seimbang mula-mula, CB = 60 cm, AC = 100 cm – 60 cm = 40 cm.
Dari syarat jembatan seimbang kita peroleh
(X)(CB) = (Y)(AC)
(X)(60 cm) = Y(40 cm)
Y = 3X/2 (*)
Keadaan sekarang, pada X disisipkan resistor 10 Ω, sehingga hambatan total = (X + 10) Ω. Ternyata jembatan seimbang jika kontak C digeser 30 cm ke kanan (mengapa tidak digeser ke kiri?). Jadi,
AC sekarang = (40 + 30) cm = 70 cm
CB sekarang = (100 – 70) cm = 30 cm
Dari syarat jembatan seimbang kita peroleh:
(X + 10)CB = (Y)(AC)
(X + 10)30 cm = Y(70 cm)
3X + 30 = 7Y (**)
3X + 30 = 7(3X/2)
2(3X + 30) = 21X
6X + 60 = 21X
–15X = –60
X = 4 Ω
Dari (*) kita peroleh Y = (3)(4 Ω)/2 = 6 Ω
Soal 4: Perhatikan gambar di atas! Panjang kawat AC 80 cm dengan R = 120 Ω. Jarum galvanmeter menunjukan angka nol pada saat kontak dengan D yang panjangnya 60 cm dari A. Tentukan besarnya Rx?
Baca Juga: Pengertian Massa Jenis - Rumus, Dan Satuan + Contoh Soalnya (LENGKAP)
Penelusuran yang terkait dengan materi JEMBATAN WHEATSTONE
- penurunan rumus jembatan wheatstone
- sejarah jembatan wheatstone
- prinsip kerja jembatan wheatstone
- teori jembatan wheatstone
- aplikasi jembatan wheatstone
- cara kerja rangkaian jembatan wheatstone
- soal jembatan wheatstone brainly
- gambar rangkaian jembatan wheatstone
Post a Comment