Materi Kinematika Dengan Analisis Vektor dan Soal Kinematika Dengan Analisis Vektor

Table of Contents

Kinematika Dengan Analisis Vektor

Kinematika adalah cabang fisika yang mempelajari gerak benda tanpa memperhatikan gaya yang menyebabkan gerak tersebut. Analisis vektor dalam kinematika membantu dalam memahami gerak dalam dua atau tiga dimensi, di mana posisi, kecepatan, dan percepatan diwakili oleh vektor. Berikut adalah beberapa konsep kinematika dengan analisis vektor:

1. Posisi: Dalam analisis vektor, posisi sebuah benda dalam ruang tiga dimensi dinyatakan oleh vektor posisi, yang menunjukkan letaknya relatif terhadap suatu titik referensi tertentu. Vektor posisi (r) dari suatu titik dapat dinyatakan sebagai perbedaan posisi antara titik tersebut dan titik referensi.

2. Perpindahan: Perpindahan adalah perubahan posisi sebuah benda dalam ruang. Dalam analisis vektor, perpindahan juga dinyatakan sebagai vektor, yang merupakan perbedaan vektor posisi akhir dan awal benda.

3. Kecepatan: Kecepatan adalah perubahan perpindahan sebuah benda per satuan waktu. Dalam analisis vektor, kecepatan juga dinyatakan sebagai vektor, yang merupakan turunan dari vektor posisi terhadap waktu. Kecepatan rata-rata adalah perubahan perpindahan dibagi dengan interval waktu.

4. Percepatan: Percepatan adalah perubahan kecepatan sebuah benda per satuan waktu. Dalam analisis vektor, percepatan juga dinyatakan sebagai vektor, yang merupakan turunan dari vektor kecepatan terhadap waktu. Percepatan rata-rata adalah perubahan kecepatan dibagi dengan interval waktu.

5. Gerak Parabola: Gerak parabola adalah gerak benda dalam ruang dua dimensi yang mengikuti pola gerak parabola. Misalnya, gerak proyektil seperti lemparan bola di udara dapat dianalisis menggunakan konsep kinematika dengan analisis vektor.

6. Gerak Melingkar: Gerak melingkar adalah gerak di mana benda bergerak mengikuti lintasan melingkar atau busur lingkaran. Analisis vektor digunakan untuk memahami parameter seperti kecepatan tangensial, kecepatan sentripetal, dan percepatan dalam gerak melingkar.

7. Gerak Relatif: Gerak relatif melibatkan gerak dua benda yang bergerak satu sama lain dalam suatu referensi. Dalam analisis vektor, posisi, kecepatan, dan percepatan relatif dihitung dengan mempertimbangkan vektor posisi dan kecepatan masing-masing benda.

8. Gaya Pusat: Gaya pusat adalah gaya yang diperlukan untuk mempertahankan gerak benda yang bergerak dalam lintasan melingkar. Dalam analisis vektor, gaya pusat diarahkan ke pusat lingkaran dan memiliki magnitudo yang sesuai dengan massa benda, kecepatan, dan radius lintasan.

Analisis vektor dalam kinematika memberikan pemahaman yang lebih mendalam tentang gerak benda dalam ruang dua atau tiga dimensi. Ini membantu dalam pemodelan dan prediksi perilaku benda dalam berbagai konteks fisika, teknik, dan ilmu alam lainnya.

GERAK LURUS

KINEMATIKA adalah Ilmu gerak yang membicarakan gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh benda selama geraknya hanya ditentukan oleh kecepatan v dan atau percepatan a.

Pada umumaya GLB didasari oleh Hukum Newton I ( S F = 0 ).

S = X = v . t ; a = Dv/Dt = dv/dt = 0

v = DS/Dt = ds/dt = tetap

Tanda D (selisih) menyatakan nilai rata-rata.

Tanda d (diferensial) menyatakan nilai sesaat.

GLBB

Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= -).

 

 

Baca Juga: Cerita Fabel Adalah - Sejarah, Ciri-ciri, Struktur Cerita Fabel, Jenis-Jenis dan Simbol Binatang Pada Cerita Fabel Beserta Contohnya

 

 

Pada umumnya GLBB didasari oleh Hukum Newton II ( S F = m . a ).

vt = v0 + a.t vt2 = v02 + 2 a S S = v0 t + 1/2 a t2

v_t = kecepatan sesaat benda
v₀ = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t

v = ds/dt = f (t) a = dv/dt = tetap

Syarat : Jika dua benda bergerak dan saling bertemu maka jarak yang ditempuh kedua benda adalah sama.

GERAK JATUH BEBAS:

y = h = 1/2 gt2 t = Ö(2 h/g) yt = g t = Ö(2 g h)

adalah gerak jatuh benda pada arah vertikal dari ketinggian h tertentu tanpa kecepatan awal (v₀ = 0), jadi gerak benda hanya dipengaruhi oleh gravitasi bumi g.

g = percepatan gravitasi bumi.
y = h = lintasan yang ditempuh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang dibutuhkan benda untuk menempuh lintasannya.

GERAK VERTIKAL KE ATAS:                           

adalah gerak benda yang dilempar dengan suatu kecepatan awal v₀ pada arah vertikal, sehingga a = -g (melawan arah gravitasi).

syarat suatu benda mencapai tinggi maksimum (h _maks): V_t = 0

Dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.

Vektor satuan.

• Vektor yang mengarah sumbu x satuannya i.
• Vektor yang mengarah sumbu y satuannya j.
• Vektor yang mengarah sumbu z satuannya k.

Vektor posisi

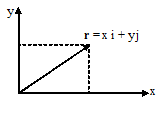Dengan r adalah vektor posisi, x menyatakan titik koordinat pada sumbu x dan y adalah titik koordinat pada sumbu y.

Vektor perpindahan

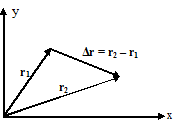Perpindahan adalah perubahan posisi suatu partikel dalam selang waktu tertentu.

Dengan Δr menyatakan vektor perpindahan dan r1 dan r2 menyatakan vektor posisi pertama dan kedua.

Vektor kecepatan rata-rata

Adalah hasil bagi antara vektor perpindahan (Δr) dengan selang waktu (Δt).

Dengan vr = vektor kecepatan rata-rata.

Vektor kecepatan sesaat

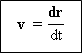
Adalah turunan pertama dari fungsi posisi (r) terhadap waktu (t).

Vektor percepatan rata-rata      

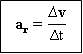Adalah perubahan kecepatan (Δv) dalam selang waktu (Δt) tertentu.

Vektor percepatan sesaat                                              

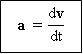Adalah turunan pertama dari fungsi kecepatan (v) terhadap waktu (t).

Menentukan vektor posisi dari vektor kecepatan.

Menentukan vektor kecepatan dari vektor percepatan.

GERAK MELINGKAR

1. GERAK MELINGKAR BERATURAN (GMB)

GMB adalah gerak melingkar dengan kecepatan sudut (w) tetap.

Arah kecepatan linier v selalu menyinggung lintasan, jadi sama dengan arah kecepatan tangensial sedanghan besar kecepatan v selalu tetap (karena w tetap). Akibatnya ada percepatan radial ar yang besarnya tetap tetapi arahnya berubah-ubah. ar disebut juga percepatan sentripetal/sentrifugal yang selalu | v. v = 2pR/T = w R ar = v2/R = w2 R s = q R

2. GERAK MELINGKAR BERUBAH BERATURAN (GMBB)

GMBB adalah gerak melingkar dengan percepatan sudut a tetap.

Dalam gerak ini terdapat percepatan tangensial a_T = percepatan linier, merupakan percepatan yang arahnya menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan v).

a = Dw/Dt = a_T / R

a_T = dv/dt = a R

T = perioda (detik)
R = jarijari lingkaran.
a = percepatan angular/sudut (rad/det²)
a_T = percepatan tangensial (m/det²)
w = kecepatan angular/sudut (rad/det)
q = besar sudut (radian)
S = panjang busur

Hubungan besaran linier dengan besaran angular:

vt = v0 + a t wt S = v0 t + 1/2 a t2

Þ w0+ a t Þ q = w0+ 1/2 a t2

Posisi sudut (θ) dan perpindahan sudut (Δθ).

Dengan Δθ menyatakan perpindahan sudut, θ1 dan θ2 menyatakan posisi sudut pertama dan kedua.

Kecepatan sudut rata-rata

Adalah hasil bagi antara perpindahan sudut (Δθ) dengan selang waktu (Δt).

Kecepatan sudut sesaat

Adalah turunan pertama dari fungsi posisi sudut (θ) terhadap waktu (t).

Vektor percepatan sudut rata-rata

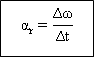Adalah perubahan kecepatan sudut (Δω) dalam selang waktu (Δt) tertentu.

Vektor percepatan sudut sesaat.

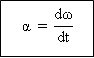Adalah turunan pertama dari fungsi kecepatan sudut (ω) terhadap waktu (t).

Menentukan posisi sudut dari kecepatan sudut.

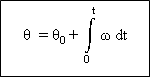
Menentukan kecepatan sudut dari percepatan sudut.

GERAK PARABOLA

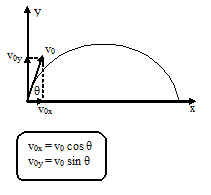
Waktu untuk mencapai ketinggian maksimum.

Ketinggian maksimum

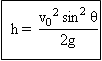
Jangkauan maksimum/jarak mendatar.

 

 

 

Soal Kinematika Dengan Analisis Vektor

---

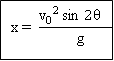
Soal 1. Sebuah partikel bergerak memenuhi persamaan posisi sebagai berikut $r\left(t\right)=(2t^2-6)i+(t^2+2t)j$ meter. Besar kecepatan setelah bergerak selama 2 detik adalah ....
A. 10 m.s^-1.
B. 8 m.s^-1
C. 6 m.s^-1
D. 4 m.s^-1
E. 2 m.s^-1
Penyelesaian Fisika: 

 

 

Soal 2. Sebuah partikel bergerak memenuhi persamaan posisi sebagai berikut $r\left(t\right)=(2t^2-6)i+(t^2+2t)j$ m. Besar kecepatan rata-rata pada selang waktu 0 sampai 2 detik adalah .... ($m.s^{-1}$)
A. 10
B. $8\sqrt{2}$.
C. 6
D. $4\sqrt{2}$.
E. $2\sqrt{5}$.

Penyelesaian Fisika

 

 

 

 

---

Soal 3. Sebuah partikel bergerak dengan vektor percepatan $a=(2i+j)m{s}^{-2}$ dengan vektor kecepatan awal $v_o=(-4i+2j)$m.s^-1 . Besar kecepatan pada detik ke 10 adalah....
A. $20\sqrt{1}$.
B. $8\sqrt{5}$.
C. $6\sqrt{2}$.
D. $4\sqrt{5}$.
E. $2\sqrt{2}$.

Penyelesaian Fisika: 

 

 

 

 

Soal 4. Sebuah partikel bergerak dengan vektor posisi $r=(t^2-4t-2)i+(0,5t^2+2t+5)j$. Besar kecepatan rata-rata setelah bergerak selama 2 detik adalah....
A. 10 m.s^-1
B. 12 m.s^-1
C. $\sqrt{13}$m.s^-1
d.$\sqrt{2}$m.s^-1
E.$2\sqrt{5}$m.s^-1

Penyelesaian Fisika:

 

 

Soal 5. Perhatikan persamaan vektor posisi di bawah ini !
$$\begin{array}{cc}r(t{)}_1& =(2t^2+2t+5)i\\ r(t{)}_2& =(t^3+5)i\end{array}$$Pernyataan yang benar adalah ....
(1) Persamaan 1 adalah gerak lurus
(2) Persamaan 2 adalah gerak lurus
(3) Percepatan persamaan 1 tetap
(4) Persamaan 2 percepatannya tetap
A. (1), (2), dan (3) benar.
B. (1), dan (3) benar.
C. (2), dan (4) benar
D. (4) saja benar
E. Semua benar

Penyelesaian Fisika:

1: Persamaan 1: $r_1=(2t^2+2t+5)i$ adalah gerak lurus berubah beraturan pada sumbu - x,

2: persamaan 2: $r_2=(t^3+5)i$ adalah gerak lurus berubah TIDAK beraturan pada sumbu x.

3: Percepatan persamaan 1: $r_1=(2t^2+2t+5)i$ adalah turunan ke 2 dari persamaan 1 terhadap t, diperoleh |a|=4$m{s}^{-2}$ tetap.

4: Percepatan persamaan 2: $(t^3+5)i$ adalah turunan ke 2 dari persamaan 2 terhadap t, diperoleh |a|=6ti$m{s}^{-2}$ berubah.

---

Soal 6.Sebuah partikel bergerak dari keadaan diam pada suatu gerak lurus. Persamaan geraknya dapat dinyatakan sebagai: $x=t^3-2t^2+3$, x dalam meter dan t dalam sekon. Kecepatan partikel pada t = 5 sekon adalah….
A. 25 m.s^-1
B. 30 m.s^-1
C. 45 m.s^-1
D. 55 m.s^-1
E. 60 m.s^-1

 

 Penyelesaian Fisika:Kecepatan turunan dari vektor posisi:

 

 

Baca Juga: Pengertian Hukum Islam Beserta Ruang Lingkup, Tujuan dan Sumber-Sumber Hukum Islam Secara Lengkap

 

Penelusuran yang terkait dengan KINEMATIKA DENGAN ANALISIS VEKTOR

• contoh soal kinematika vektor
• kinematika dengan analisis vektor - pdf
• contoh soal vektor kecepatan dan percepatan
• contoh soal kinematika kuliah
• kinematika partikel
• resume kinematika
• makalah kinematika dengan analisis vektor
• rumus perpindahan vektor